Stimmgerät was nun? – Teil 1

Ich habe Erklärungen gesucht für die gemachten Beobachtungen in den Artikeln „Verwirrende Stimmbeobachtung“ und den dazugehörigen Teil 2. Warum sind die Messergebnisse durch Obertöne beeinflussbar?

Ich greife auf Wikipedia zurück, um das Grundproblem zu erklären. In dem Wikipediaartikel Ton (Musik) steht:

Unter Klang versteht man in der Physik ein periodisches aus Sinustönen zusammengesetztes Schallereignis, bei dem die Frequenzen der Teiltöne in einem ganzzahligen Verhältnis zueinander stehen, sich also „harmonisch“ zueinander verhalten. Hierbei handelt es sich jedoch um ein vereinfachtes Modell, das auf reale Klänge nur näherungsweise angewendet werden kann.

Reale Klänge sind nämlich im Allgemeinen komplexer, wobei Geräuschkomponenten und Inharmonizitäten eine wichtige Rolle spielen.

Jetzt wird es mathematisch. Vielleicht kann sich so mancher erinnern, wenn ich Sinuswellen haben, die in ganzzahligen Vielfachen zur tiefsten Sinuswelle schwingen, dass die Nullstellen des tiefsten Ton mit einer Nullsteller der höheren Frequenzen zusammenfallen müssen. Da ist sogar die Stärke der Obertöne egal.

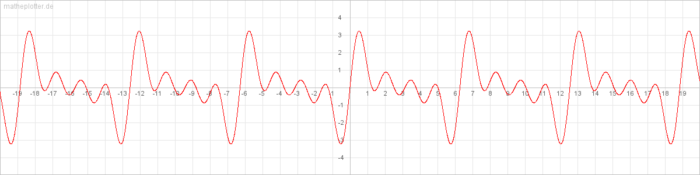
Dazu die beiden Graphen der Funktionen. (Um die Graphen besser zu sehen, draufklicken.)

• • F(x)= sin(1x)+sin(2x)+sin(3x)+sin(4x) (harmonische Schwingungen)
    

• F(x)= sin(1x)+0,5*sin(2x)+0,7*sin(3x)+0,9*sin(4x) (harmonische Schwingungen mit unterschiedlicher Maximalamplitude)
  

Auch wird deutlich, wir haben immer ein schönes sich wiederholendes Muster, dessen Zeitdauer exakt gleich ist.

Sobald die Frequenzen keine ganzzahligen Vielfachen sind, also inharmonisch sind, entstehen keine periodischen Muster.

Zur Verdeutlichung die Graphen der Funktionen

• • F(x)= sin(1x)+sin(2,22x)+sin(3,33x)+sin(4,44x) (Inharmonische Schwingungen)
    

• F(x)= sin(1x)+0,5*sin(2,22x)+0,7*sin(3,33x)+0,9*sin(4,44x) (Inharmonische Schwingungen mit unterschiedlicher Maximalamplitude)
  

Legt man nun den Graphen der ersten Funktion und der letzten Funktion übereinander, dann sieht man, dass diese Graphen keine einzige Nullstelle gemeinsam haben, obwohl sie die gleiche Grundfrequenz haben. Aber diese Nullstellen sind wichtig, um die Grundfrequenz also Tonhöhe zu bestimmen.

Also bei einem idealen Ton ist die Zeitdauer der Periodenänderung durch die Nullstellen einfach feststellbar, bei einem echten Ton mit Inharmonizität schwierig.

Jetzt habe ich, um das Grundproblem deutlich zu machen, Werte verwendet, die deutlich über das hinausgehen, was Inharmonizität bedeutet. Dabei war habe ich auch noch keine Dämpfung eingebaut.

Die Frage ist, was macht ein Stimmgerät aus diesem Problem?

Deswegen habe ich versucht, herauszufinden wie Stimmgeräte funktionieren. Die eine Variante ist ein Frequenzzähler oder FFT (Schnelle Fourier-Transformation).

Ein Frequenzzähler arbeitet mit den Nullstellen. Damit wird klar, warum man ihn mit Inharmonizität oder inharmonischen Obertönen beeinflussen kann.

Was ist jetzt mit FFT? Mit FFT kann man eine komplexe Welle in ihre Einzelwelle zerlegen. Aber es ist ein Annäherungsverfahren. Eine richtige Fourier-Transformation soll extrem viel Rechenpower brauchen.

Ich habe leider keine fachkundige Antwort erhalten, ob Inharmonizität und die unterschiedliche Dämpfung der Obertöne das Ergebnis für die Bestimmung des Grundtones beeinträchtigen oder beeinflussen. Und das selber auszurechnen ist mir dann doch deutlich zu hoch.

Aber ich bin im Netz auf Threads gestoßen, von Leuten, die ihre eigene Stimmanwendung programmieren wollten. Es ging darum, wie man die FFT am klügsten gestaltet.

Ein Thread fiel mir aber besonders auf. Das Problem des Programmierers war, dass seine Software für die mittleren Saiten seines Klaviers dieselben Werte wie sein Stimmgerät anzeigte, aber bei den tiefen Saiten deutlich andere Ergebnisse anzeigte.

Tiefe Klaviersaiten sind deutlich dicker als die mittleren Klaviersaiten. Damit ist aber auch die Inharmonizität der tiefen Klaviersaiten deutlich höher.

Deswegen bin ich mir ziemlich sicher, dass Inharmonizität auch ein Problem für Stimmgeräte ist, die auf FFT basieren.

Was das nun für die Verwendung eines Stimmgerätes bedeutet, dazu äußere ich mich nächste Woche.

Der Beitrag wurde am Freitag, den 25. Januar 2019 um 08:04 Uhr veröffentlicht von Stephan Zitzmann und wurde unter den Kategorien: Elektronik, Gehör, Gitarre lernen, Gitarre stimmen, Gitarrenunterricht, Musiktheorie, Software abgelegt. | Es gibt keinen Kommentar .